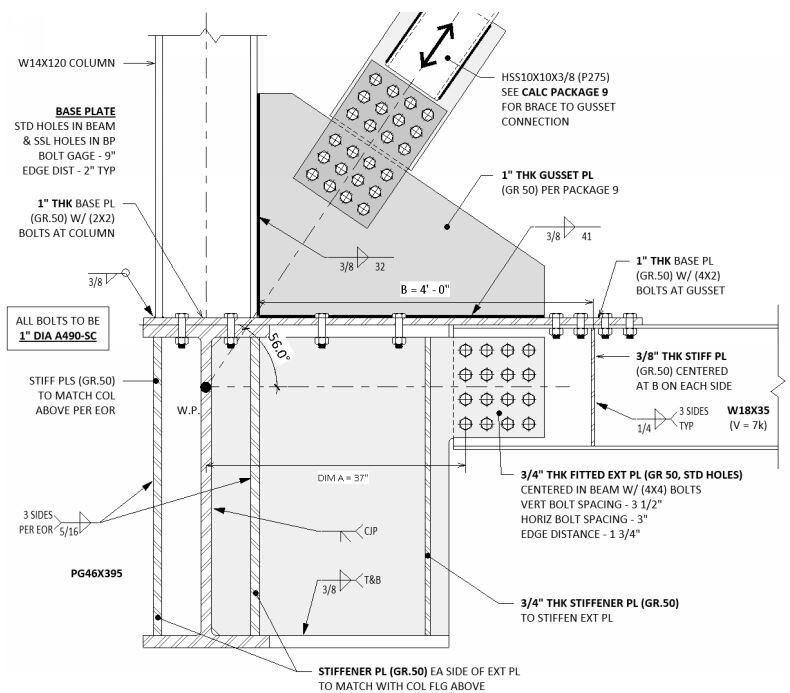
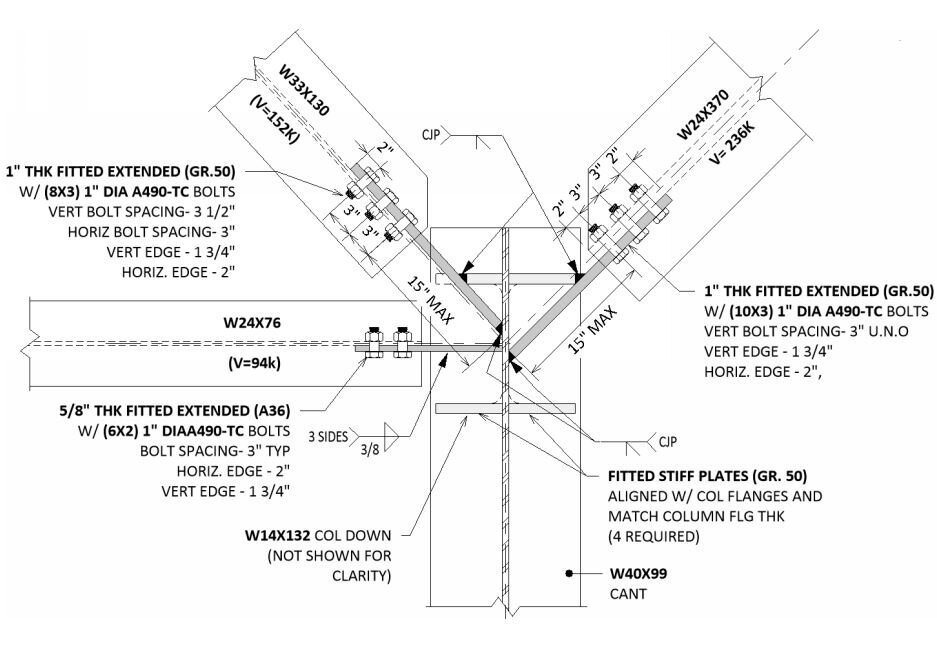
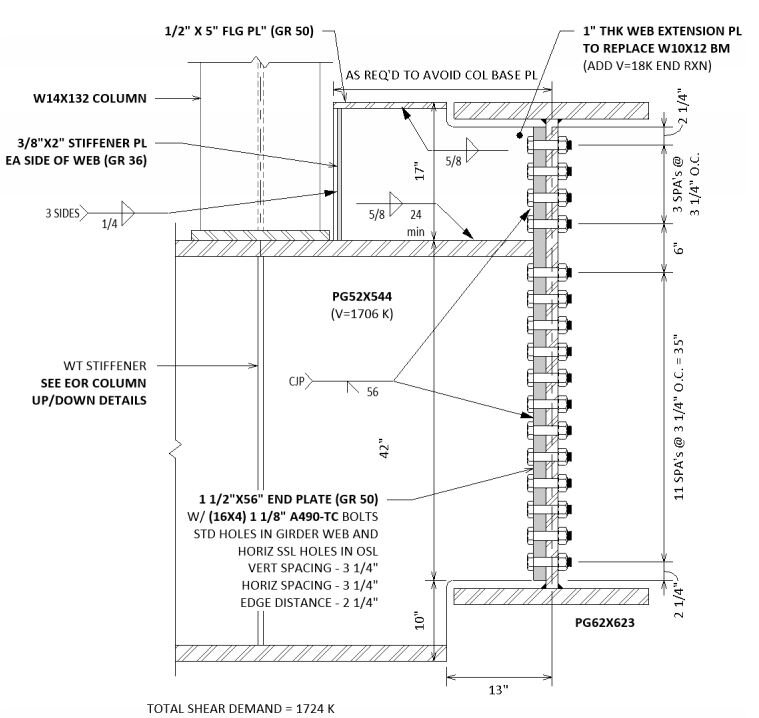
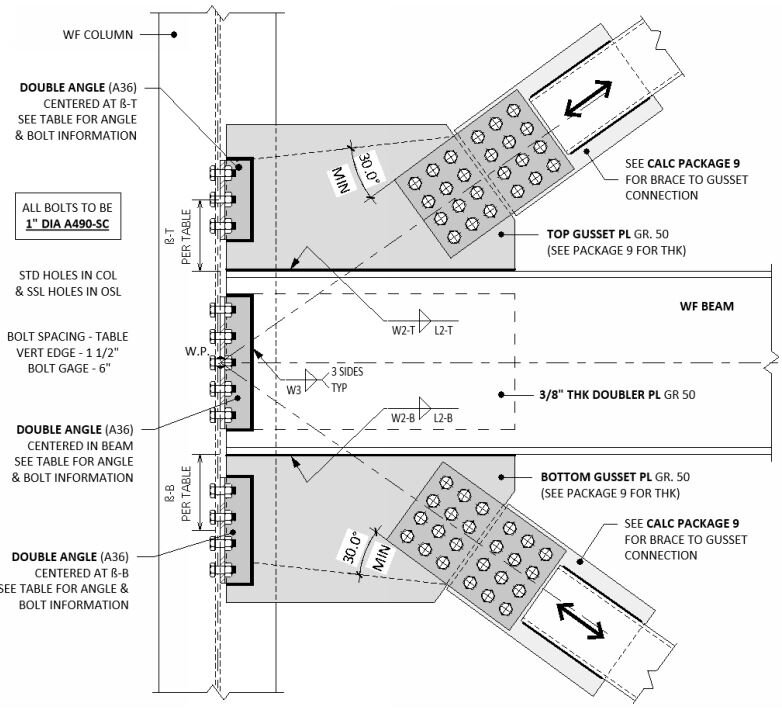
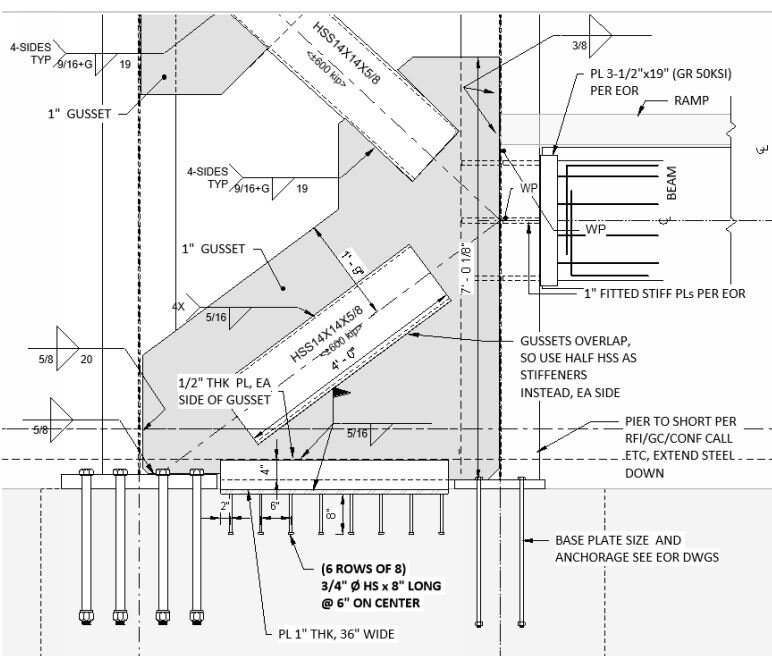
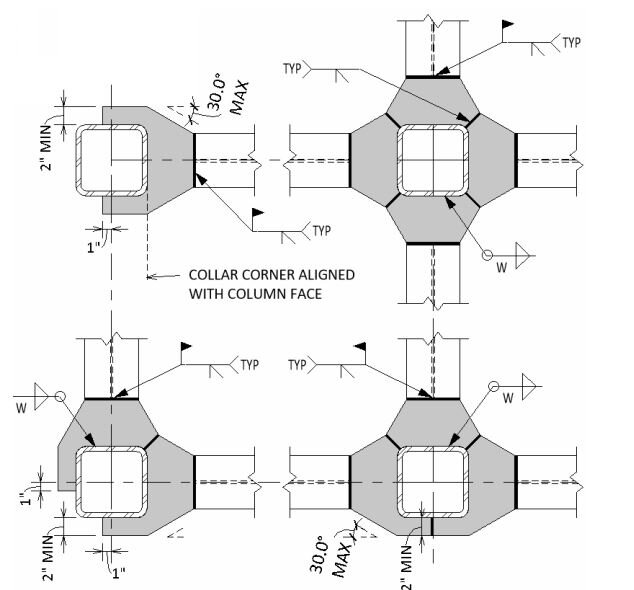
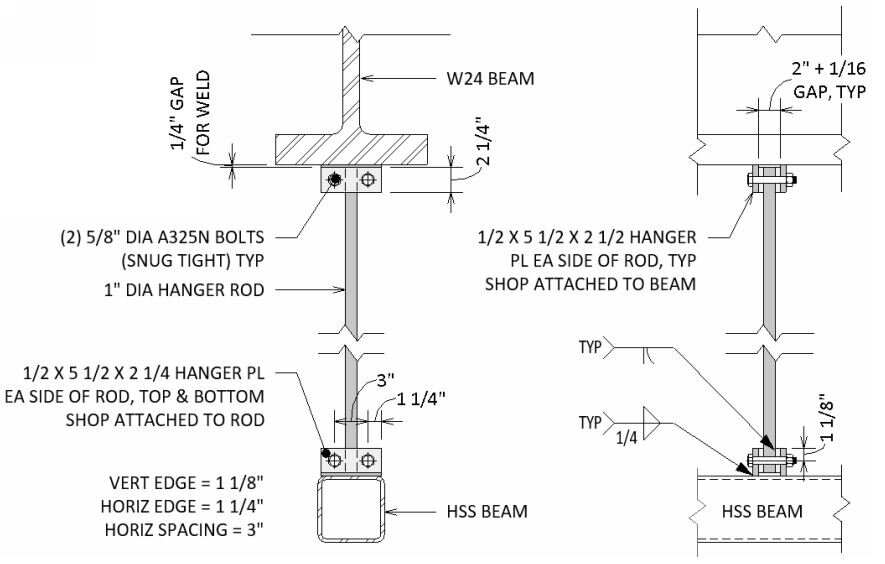
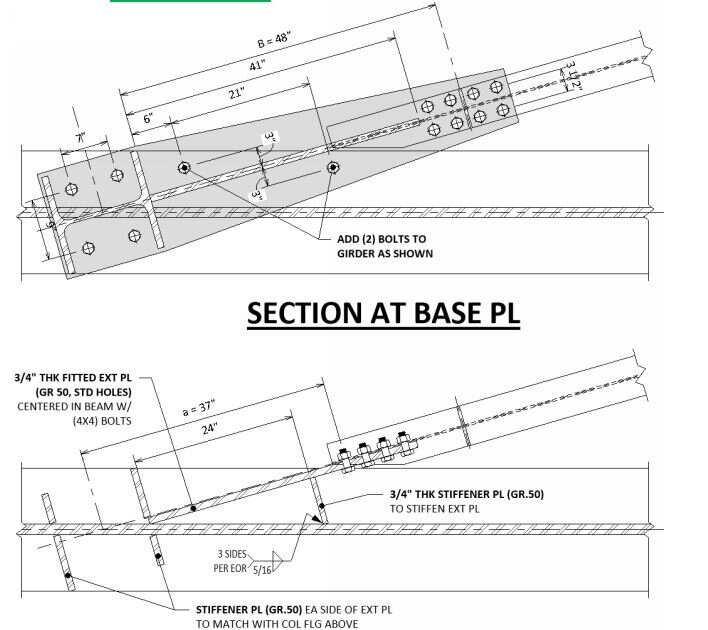
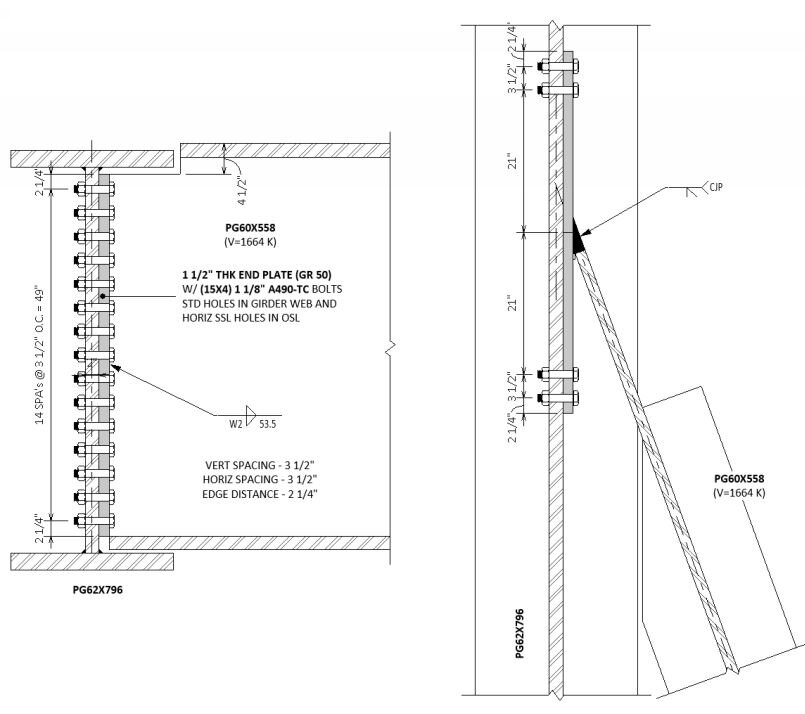
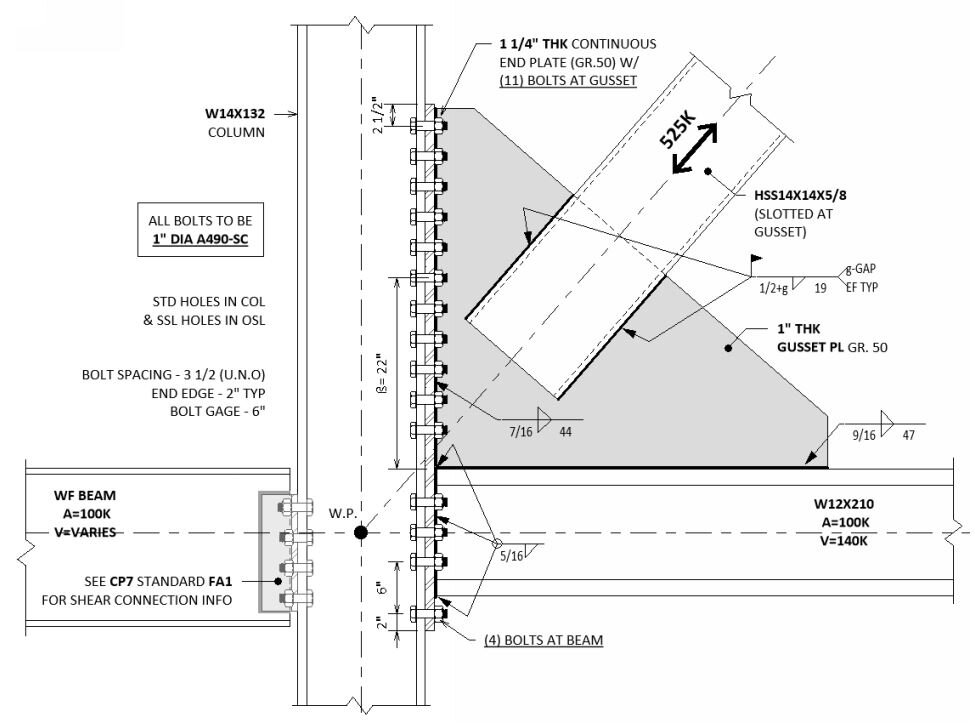
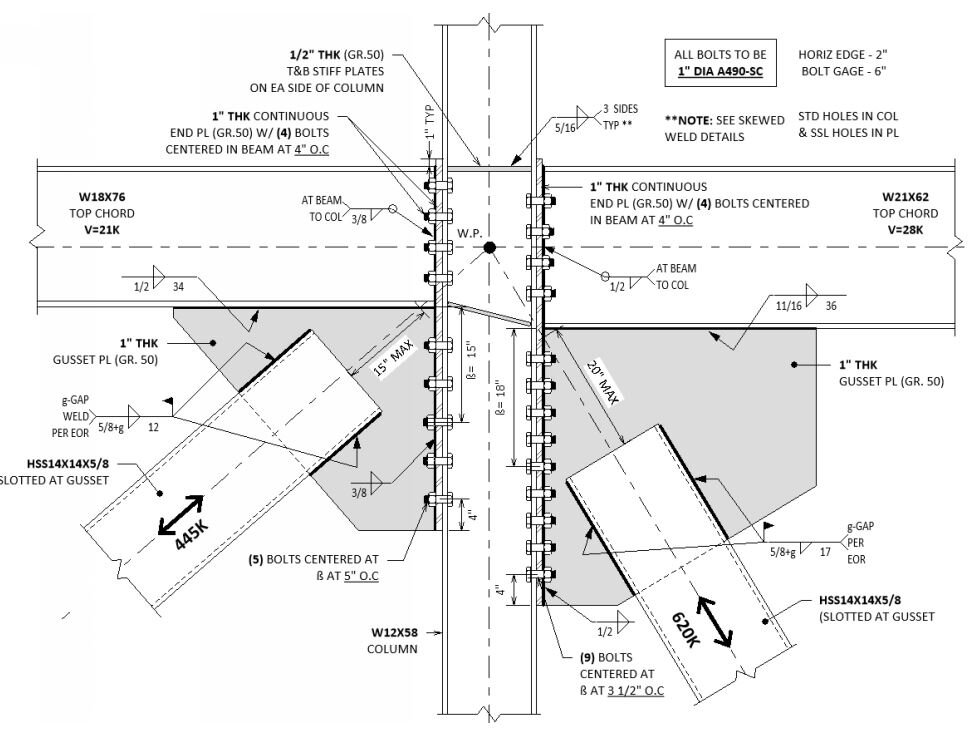
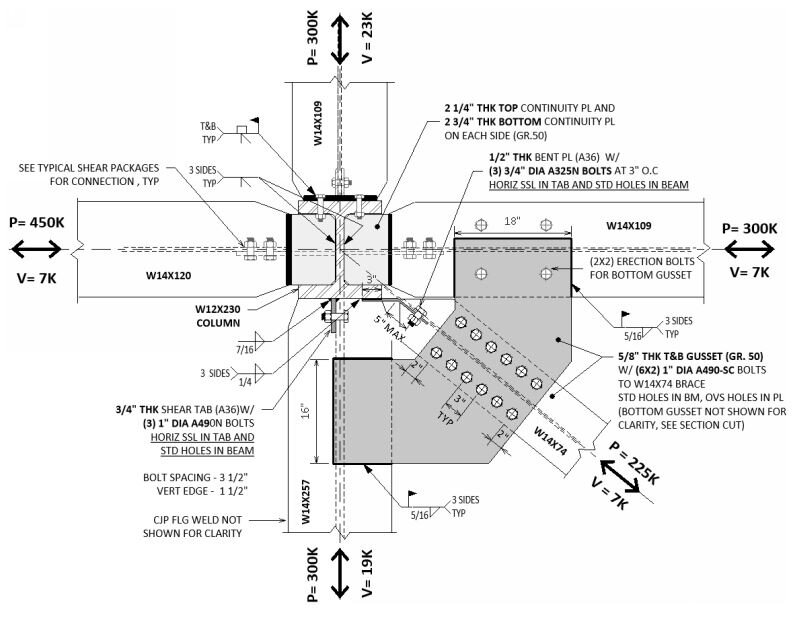
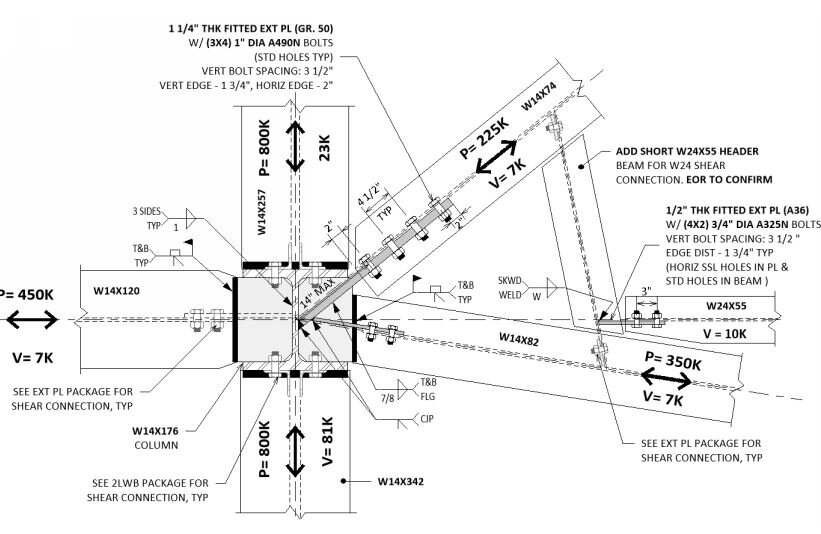
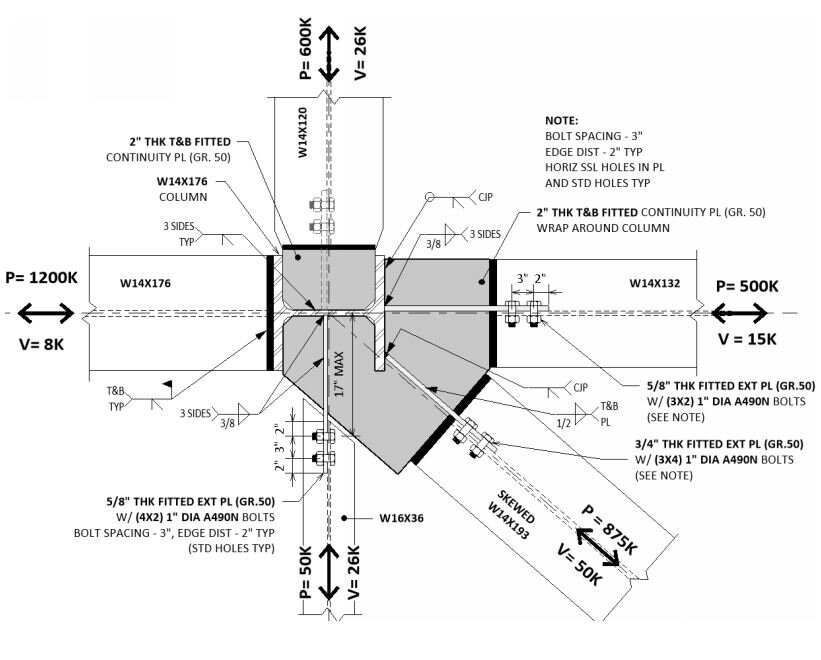
The trees do speak to us,
Their whispers carried by the wind—
Leaves brushing leaves,
Crafting melodies we name silence.
They are not our trees. They never were.
They are simply the trees,
Guardians of epochs long before humanity's dawn,
Their lives stretching beyond our fleeting existence—
Some standing tall for over four millennia.
We felled the eldest, yet spared the second—
Can the second ascend to ancient heights,
Or shall we deny it that legacy?
Once wild, now tamed and farmed,
A monolithic “conserved” forest can never replace the untamed.
Weyerhaeuser’s promises lie hollow,
Conservation is not preservation!
As divergent as Pinchot and Muir—
For Pinchot, nature was a resource,
To be stewarded and shared for human gain.
For Muir, nature was sacred,
Best preserved in untouched sanctuaries,
Far from humanity’s degrading grasp.
Let trees be preserved in their tangled diversity,
Left untouched to thrive beyond our reach.
Trees are not solitary beings. They are collective,
There is no single tree, only forests—
Living, breathing symphonies of existence.
They flourish through connection,
Roots entwining beneath the earth,
An intricate network beneath our feet and above our heads,
Communities interwoven.
We have much to learn from their silence.